Approximated Cosine in C annotated in ACSL

This is a C version of the Approximated Cosine example, annotated in ACSL

Topics: Floating-Point Computations / Non-linear Arithmetic

Tools: Frama-C / Jessie / Gappa / Coq

see also the index (by topic, by tool, by reference, by year)

Here is the consider annotated code. Explanations follows

/*@ requires \abs(x) <= 0x1p-5;
  @ ensures \abs(\result - \cos(x)) <= 0x1p-23;
  @*/
float my_cos1(float x) {
  //@ assert \abs(1.0 - x*x*0.5 - \cos(x)) <= 0x1p-24;
  return 1.0f - x * x * 0.5f;
}

/*@ requires \abs(x) <= 0x1p-5
  @     && \round_error(x) == 0.0;
  @ ensures \abs(\result - \cos(x)) <= 0x1p-23;
  @*/
float my_cos2(float x) {
  float r = 1.0f - x * x * 0.5f;
  //@ assert \abs(\exact(r) - \cos(x)) <= 0x1p-24;
  return r;
}

/*@ requires \abs(\exact(x)) <= 0x1p-5
  @     && \round_error(x) <= 0x1p-20;
  @ ensures \abs(\exact(\result) - \cos(\exact(x))) <= 0x1p-24
  @     && \round_error(\result) <= \round_error(x) + 0x3p-24;
  @*/
float my_cos3(float x) {
  float r = 1.0f - x * x * 0.5f;
  //@ assert \abs(\exact(r) - \cos(\exact(x))) <= 0x1p-24;
  return r;
}

/*@ requires \abs(x) <= 0.07 ;
  @ ensures \abs(\result - \cos(x)) <= 0x1p-20;
  @*/
float my_cos4(float x) {
  //@ assert \abs(1.0 - x*x*0.5 - \cos(x)) <= 0x0.Fp-20;
  return 1.0f - x * x * 0.5f;
}

1 Description

The program above provides various approximations of the cosine function on small intervals around 0.

Using Frama-C/Jessie with the strict-IEEE float model, we specify bounds on the total error expected from each function. An assertion in the code is inserted in each function, to express the mathematical error, that is without taking rounding in account.

The third function assumes that the argument is given with an already non-null rounding error, and the error on the result is given in terms of this rounding error on input.

2 Proof process

The C file above can be analyzed by Frama-C/Jessie using

frama-c -jessie my_cosine.c

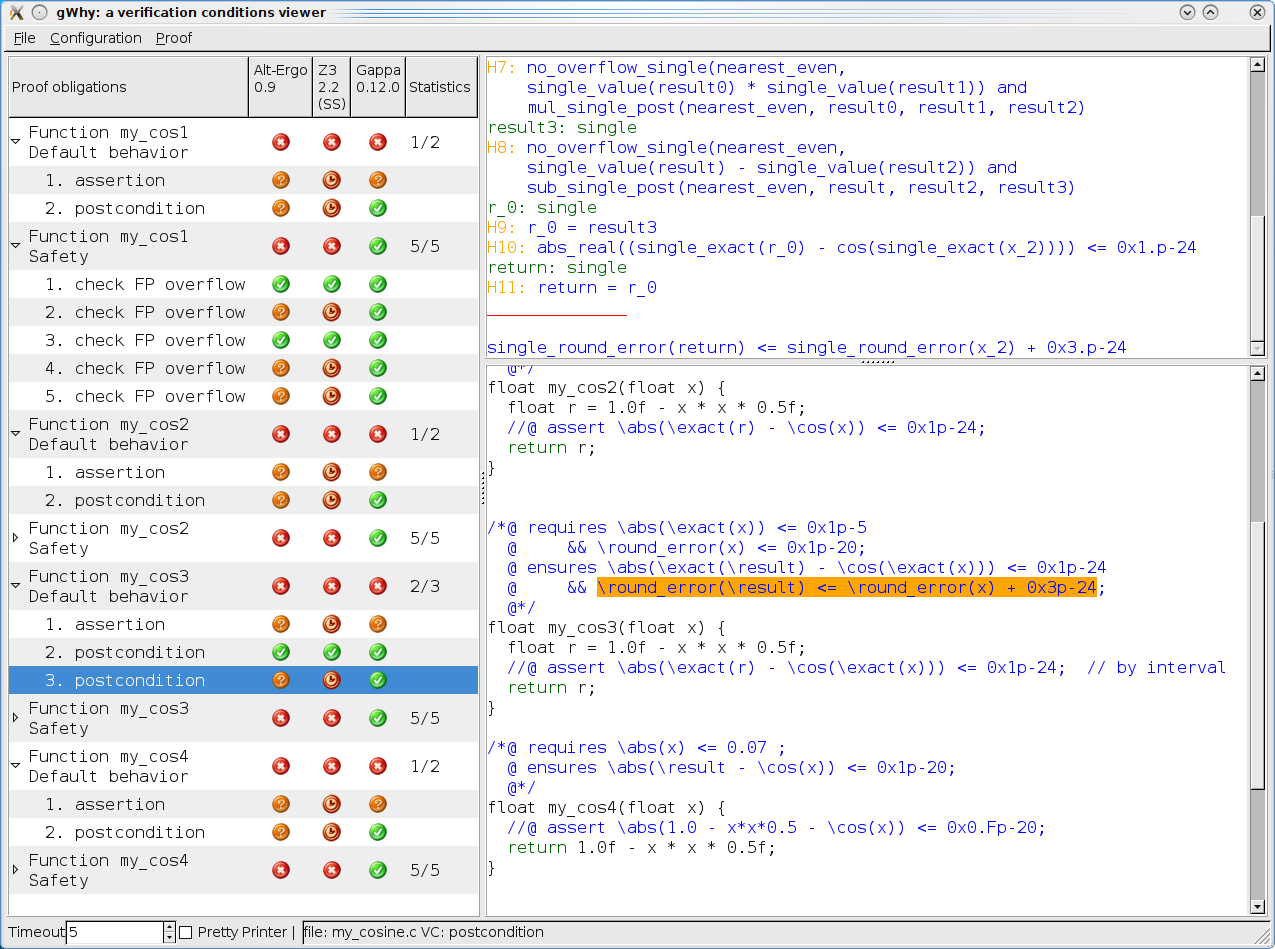
Verification conditions are proved by a combination of automated provers (SMT solvers and Gappa and the Coq proof assistant.

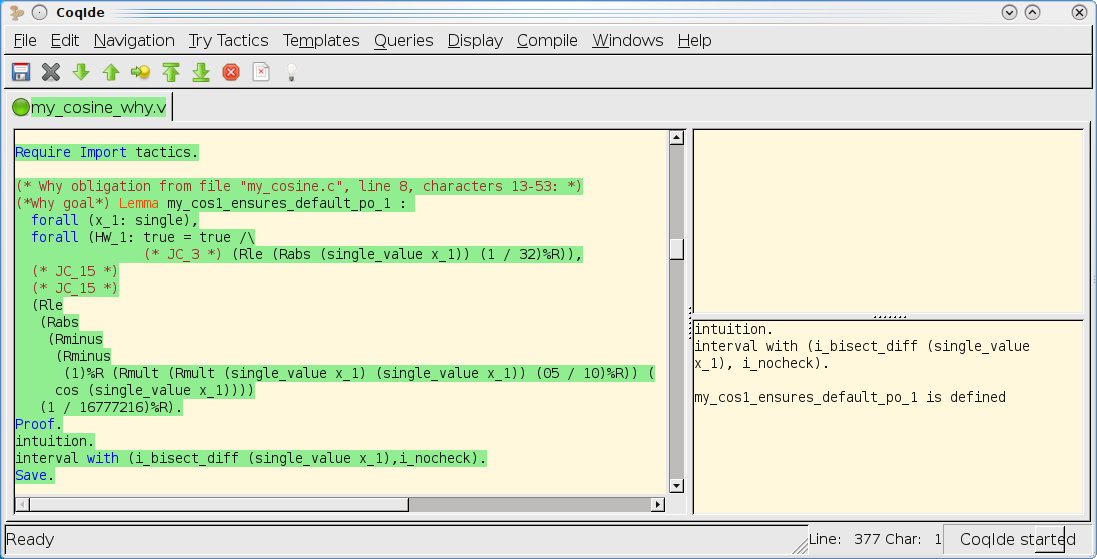
The following screenshot shows that SMT solvers and Gappa verify all verification conditions except the mathematical method errors. The latter are verified inside Coq using the interval tactic, shown on the second screenshot below.

Coqide screenshot of proof of first verification condition:

Toccata

Formally Verified Programs, Certified Tools and Numerical Computations